Перестановки
Перевод статьи - Permutations
Автор(ы) - Филипп Эрдельский (Philip J. Erdelsky)
Источник оригинальной статьи:
Филипп Эрдельский
13 ноября 2006 г.
Пожалуйста, присылайте комментарии, исправления и дополнения веб-мастеру по адресу [email protected].
1. Введение
Перестановка множества - это способ перестановки элементов множества. Например, {1,2} и {2,1} являются двумя перестановками множества {1,2} .
Набор {1,2,3} имеет шесть перестановок: {1,2,3}, {1,3,2}, {2,1,3}, {2,3,1}, {3,1, 2} и {3,2,1} .
Перестановка также может быть определена более формально как взаимно-однозначное соответствие набора с самим собой, функция, которая переносит каждый элемент набора в тот, который занимает ту же позицию после применения перестановки. Например, перестановка {1,3,2} - это функция f: {1,2,3} ⟶ {1,2,3} с f (1) = 1, f (2) = 3 и f (3 ) = 2 или множество {(1,1), (2,3), (3,2)} . Такой способ мышления перестановок особенно полезен, если элементы множества не имеют естественного порядка.
Иногда перестановка иллюстрируется показом набора до и после перестановки со стрелкой от каждого элемента к его новой позиции. Например, перестановки {1,3,2} и {2,1,3}могут быть проиллюстрированы следующим образом:
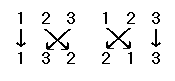
Идентификационная перестановка набора - это перестановка, которая оставляет набор неизменной, или функция, которая отображает каждый элемент на себя. В нашем примере тождественная перестановка равна {1,2,3} .
2. Состав перестановок
Композиция двух перестановок одного и того же набора является просто композицией связанных функций. Например, перестановки {1,3,2} и {2,1,3} могут быть составлены путем отслеживания пункта назначения каждого элемента.
| Начать с этот элемент |
Он сопоставлен с {1,3,2} к этому элементу |
который отображается {2,1,3} к этому элементу |
|---|---|---|
| 1 | 1 | 2 |
| 2 | 3 | 3 |
| 3 | 2 | 1 |
Следовательно, {1,3,2} ◌ {2,1,3} = {2,3,1} .
Аналогично, можно показать, что {2,1,3} ◌ {1,3,2} = {3,1,2}
| Начать с этот элемент |
Он сопоставлен с {2,1,3} к этому элементу |
который отображается {1,3,2} к этому элементу |
|---|---|---|
| 1 | 2 | 3 |
| 2 | 1 | 1 |
| 3 | 3 | 2 |
Этот простой пример показывает, что композиция не обязательно коммутативна (но она ассоциативна).
Операции могут быть показаны более четко в графической форме:
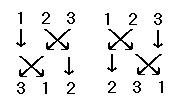
Если I - тождественная перестановка, а P - любая перестановка из того же набора, то ясно, что I ◌ P = P ◌ I = P. Существует также обратная перестановка P -1, для которой P -1 ◌ P = P ◌ P -1 = I. Это можно найти, взяв функционал, обратный к нему, или обращая каждую упорядоченную пару в определении функции как набор упорядоченных пар (и затем сортируя упорядоченные пары по их новым первым элементам).
Например, обратное к {2,3,1} является обратным к {(1,2), (2,3), (3,1)} , то есть {(2,1), (3,2 ), (1,3)} или {(1,3), (2,1), (3,2)} или {3,1,2} .
Хотя состав перестановок в общем случае не является коммутативным, он является коммутативным, когда одной из перестановок или результатом является тождество.
3. Четные и нечетные перестановки
Пусть p - перестановка множества S = {1,2,3, ..., n} (или любого другого полностью упорядоченного конечного множества). Рассмотрим пару (i, j) элементов в S, для которых i .Если p (i)> p (j), то говорят, что перестановка инвертирует порядок (i, j) .
Число таких пар, инвертированных перестановкой, не является очень полезным свойством перестановки, но то, является ли число четным или нечетным, оказывается полезным свойством, называемым четностью перестановки. Если перестановка инвертирует четное количество таких пар, она называется четной перестановкой ; если он инвертирует нечетное количество таких пар, то говорят, что это нечетная перестановка .
Тождественная перестановка очевидно четна; {2,1} является примером нечетной перестановки.
Хотя может показаться, что определение четных и нечетных перестановок зависит от упорядоченности множества, мы докажем, что это не так.
Обмен - это перестановка, которая обменивает два элемента и оставляет все остальные элементы неизменными.
Лемма 3.1. Транспонирование двух элементов перестановки конечного множества, что эквивалентно составлению его с обменом, превращает четную перестановку в нечетную перестановку и наоборот.
Доказательство. Сначала установим лемму для двух смежных элементов.
Пусть {p (1), p (2), ..., p (n)} - перестановка {1,2, ..., n} , а k - целое число от 1 до n-1 , включительно. Тогда перестановка {p (1), p (2), ..., p (k + 1), p (k), ..., p (n)} является перестановкой с двумя смежными элементами p (k) и p (k + 1) поменялся.
При подсчете инвертированных пар в новой перестановке мы видим, что все пары, которые были инвертированы в старой перестановке, также инвертированы в новой перестановке, и наоборот, кроме пары (k, k + 1) , которая изменяется от инвертированной неинвертированным или наоборот. Следовательно, число инвертированных пар в новой перестановке на 1 больше или меньше числа в старой перестановке. Это устанавливает лемму для смежных пар.
Теперь пусть i и j будут двумя непоследовательными целыми числами от 1 до n включительно, где i , и рассмотрим перестановку, в которой были заменены p (i) и p (j) . Мы можем сделать это с помощью серии обменов последовательных элементов. Мы перемещаем p (i) на j-ю позицию путем ji обмена последовательными элементами. Сначала мы меняем p (i) на p (i + 1) , затем мы меняем p (i) (который сейчас находится в (i + 1) -й позиции) на p (i + 2) и так далее, пока p (i) достигает положения, ранее занимаемого p (j) .Следующий пример, в котором i = 5 и j = 9 , должен прояснить этот процесс:
р (5), р (6), р (7), р (8), р (9)
----------
обмен
р (6), р (5), р (7), р (8), р (9)
----------
обмен
р (6), р (7), р (5), р (8), р (9)
----------
обмен
р (6), р (7), р (8), р (5), р (9)
----------
обмен
р (6), р (7), р (8), р (9), р (5)
Затем мы выполняем аналогичную последовательность обменов j-i-1 в противоположном направлении, чтобы переместить p (j) вниз в положение, ранее занимаемое p(i) . В нашем примере:
р (6), р (7), р (8), р (9), р (5)
----------
обмен
р (6), р (7), р (9), р (8), р (5)
----------
обмен
р (6), р (9), р (7), р (8), р (5)
----------
обмен
р (9), р (6), р (7), р (8), р (5)
Результатом является исходная перестановка с замененными p (i) и p (j) и другими элементами в их исходных положениях. Число обменов последовательных элементов равно (ji) + (ji-1) , что нечетно. Поэтому перестановка была изменена с четного на нечетный или наоборот.
Обратите внимание, что эта лемма применяется только в том случае, если обмен применяется после перестановки. Однако ясно, что обмен i с j до перестановки p эквивалентен обмену p (i) и p (j) после перестановки. Следовательно, лемма применима в любом случае.
Теорема 3.2. Каждая перестановка представляет собой композицию обменов и является четной перестановкой, если и только если число обменов является четным.
Доказательство. Пусть {p (1), p (2). ..., p (n)} - перестановка. Начните с {1,2, ..., n} . Если p (1) не равно 1 , то один обмен приведет его к первой позиции. Если p (2) не равно 2 , то один обмен приведет его ко второй позиции. Поступая таким образом, мы можем получить {p (1), p (2). ..., p (n)} как композиция обменов. Другая часть является следствием леммы 3.1.
Обратите внимание, что эта характеристика нечетных и четных перестановок не зависит от порядка элементов.
Следствие 3.3. Композиция двух перестановок конечных множеств четна тогда и только тогда, когда обе перестановки являются четными или обе нечетными.
Следствие 3.4. Перестановка конечного множества и его инверсия являются четными или нечетными.
Теорема 3.5. Конечное множество с двумя или более элементами имеет одинаковое количество четных и нечетных перестановок.
Доказательство. Для каждой четной перестановки мы можем получить уникальную нечетную перестановку, переставив первые два элемента. Это определяет взаимно-однозначное соответствие между четными и нечетными перестановками, следовательно, есть равные числа каждого.
Перестановка может оставить некоторые элементы набора фиксированными. Например, {1,3,2,5,4} является четной перестановкой, которая оставляет элемент 1 фиксированным.Если мы рассмотрим только влияние на {2,3,4,5} , мы получим перестановку из четырехэлементного набора, которая также является четной. Следующая теорема дает более общий результат.
Теорема 3.6. Если перестановка оставляет один или несколько элементов фиксированными, то перестановка, ограниченная другими элементами, имеет ту же четность, что и исходная перестановка.
Доказательство. Ограниченная перестановка может быть разложена на ограниченные обмены. Эти обмены, когда они распространяются на весь набор, дают исходную перестановку. Следовательно, обе перестановки являются четными или нечетными.
4. Пазл из пятнадцати плиток
Популярная головоломка включает в себя набор из 15 скользящих плиток в квадрате 4 × 4:
1 2 3 4
5 6 7 8
9 10 11 12
13 14 15
Шестнадцатая позиция пуста. Плитки можно переставить, переместив соседние плитки в заготовку. Посредством повторяющихся движений такого рода мы можем переставлять плитки, как в этом примере:
1 2 3 4 1 2 3 4 1 2 3 4
5 6 7 8 5 6 7 8 5 6 7 8
9 10 11 12 9 10 11 12 9 10 12
13 15 14 13 15 14 13 15 11 14
1 2 3 4 1 2 3 4
5 6 7 8 5 6 7 8
9 10 12 9 10 12 14
13 15 11 14 13 15 11
Предположим, мы хотим получить следующий результат:
1 2 3 4
5 6 7 8
9 10 11 12
13 15 14
Легко показать, что это невозможно. Каждое расположение представляет собой перестановку из шестнадцати элементов, где пробел рассматривается как шестнадцатый элемент.Каждый ход предполагает обмен плиткой с пустым пространством. Количество ходов должно быть четным, потому что пробел должен двигаться вверх и вниз на одинаковое количество пробелов, а правый и левый равные числа пробелов, если он должен быть возвращен в исходное положение в нижнем правом углу.
Желаемый результат - нечетная перестановка, так как он является результатом одного обмена. Следовательно, оно не может быть достигнуто указанным способом.